こどもたちにピタゴラスの定理を発見してもらう方法

直角三角形の3辺の長さに関する $a^2+b^2=c^2$ という関係は三平方の定理（ピタゴラスの定理）と呼ばれます。この定理は文科省のカリキュラムでは中学3年生（14-15歳）で学ぶ内容です。一方、モンテッソーリ教育では早ければ小学4年生（9歳）頃¹に学びます。

説明ではなく体験を通して理解する

文科省の従来のカリキュラムでは、こどもたちは、教師の説明を聞いて三平方の定理を理解することを求められます。理解度を試すテストがあり、このテストに合格することで理解したとみなされます。公式を暗記して特定のテスト問題を解けているだけだとしても、つまり、理を解していなくても、テストの点数が十分高ければ理解したとみなされるのです。

一方、モンテッソーリ教育では、こどもたちは、教具と呼ばれるユニークな学習教材を気の向くままに遊んで三平方の定理を発見的に理解します。こどもは知らず知らずの内に『原論』の著者である数学者エウクレイデス²のように、自力で定理を証明する体験をしてしまうのです。

三平方の定理を学ぶためのモンテッソーリ教具

三平方の定理を学ぶためのモンテッソーリ教具（Nienhuisサイトより引用）

この教具は3種類のパズルになっていて、それぞれが以下の場合の三平方の定理の証明になっています。

① 直角二等辺三角形の場合
② 辺の長さが3:4:5の直角三角形の場合
③ 全ての直角三角形の場合

以下に具体的な説明をします。

三平方の定理の教具工作キット

と思いましたが、数学的な説明はややこしくてわかりにくいので、体験を通して直感的にわかってもらえるよう工作キットを作成しました。常識の範囲内で、自由に使ってください。

• 教具工作キット①のPDFをダウンロード
• 教具工作キット②のPDFをダウンロード
• 教具工作キット③のPDFをダウンロード

注記

このキットは クリエイティブ・コモンズ 表示 - 非営利 - 改変禁止 4.0 ライセンスの下に提供されています。

3つのファイルが3種類のパズルに対応しています。それぞれのPDFは、3ページで構成されています。1ページ目は色付きなので印刷して切り取るだけで使えます。2ページ目は白黒なので色塗りをする必要があります。3ページ目は白黒で、ガイドとして色の指定の印が入っています。お好きなページを使って、教具を作ってみてください。厚紙に印刷すると使いやすいです。

工作キットの使い方

ここからは工作キットを印刷して手元にあることを前提に説明します。

① 直角二等辺三角形の場合

それでは、1つ目のパズルを見ていきます。
工作キット①で作成した教具を使います。
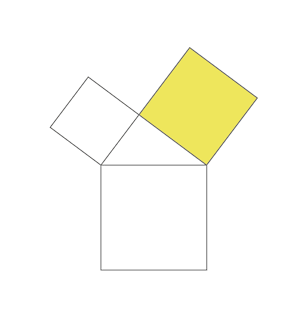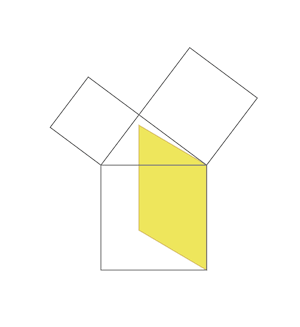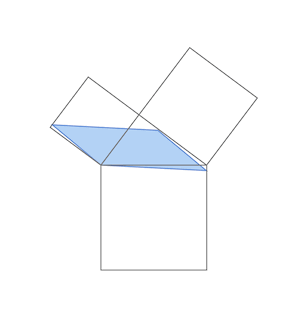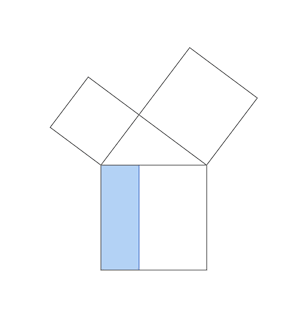
次の図で全てのピースが揃っているか確認できます。

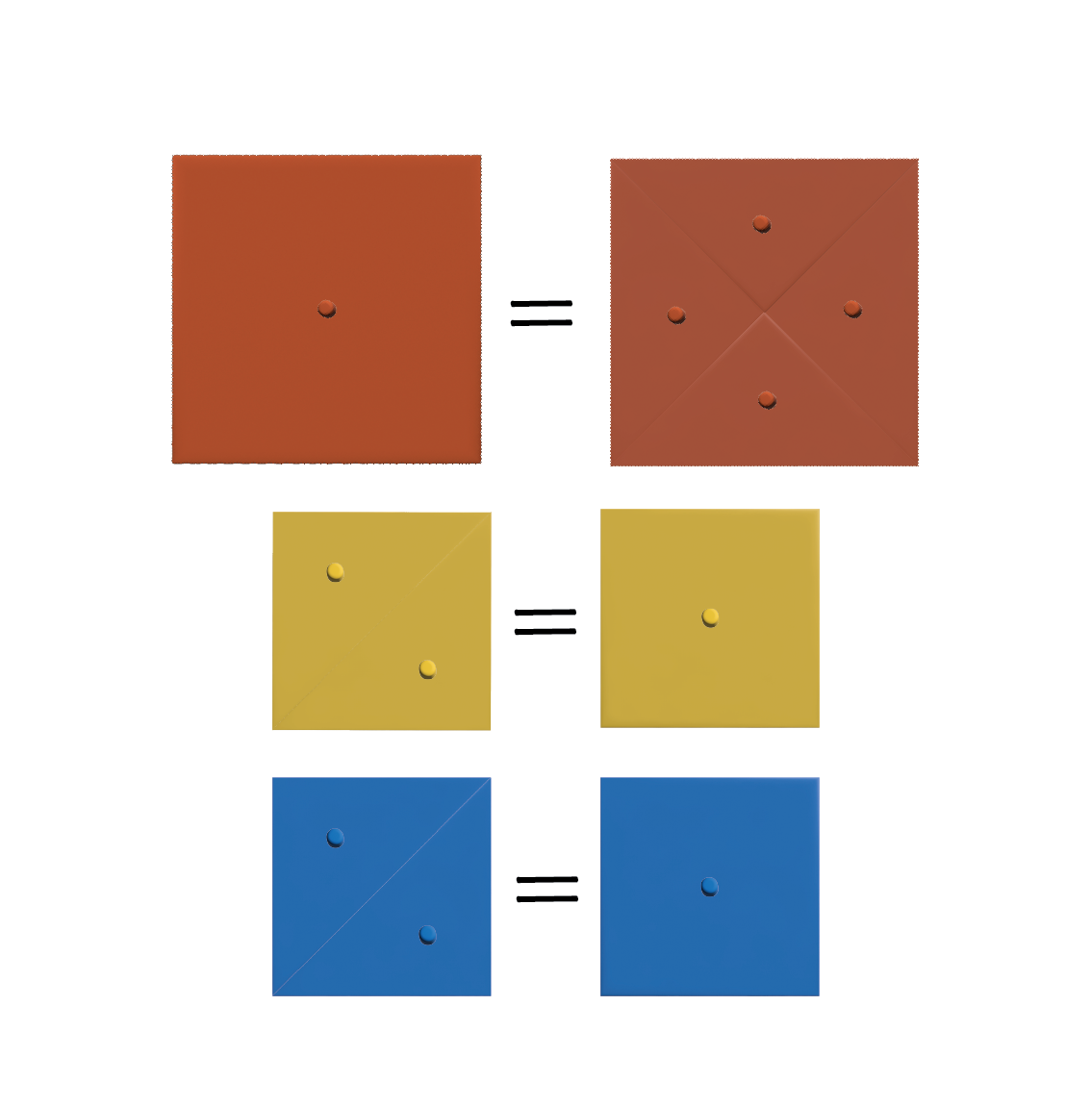
最初に緑の枠に白の直角二等辺三角形と3色の正方形がピッタリとはまることを確認します。

次に３色の正方形がそれぞれの色の二等辺三角形と置き換えられることを確認します。

ここまでで、以下のことがわかりました。

• 大きな赤の正方形の面積 $=$ 赤の直角二等辺三角形4つの面積
• 黄色の正方形の面積 $=$ 黄色の直角二等辺三角形2つの面積
• 青の正方形の面積 $=$ 青の直角二等辺三角形2つの面積

最後に赤の二等辺三角形と青・黄色の二等辺三角形を交換してもピッタリとはまることを確認します。

以上で次のことがわかります。

• 大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積

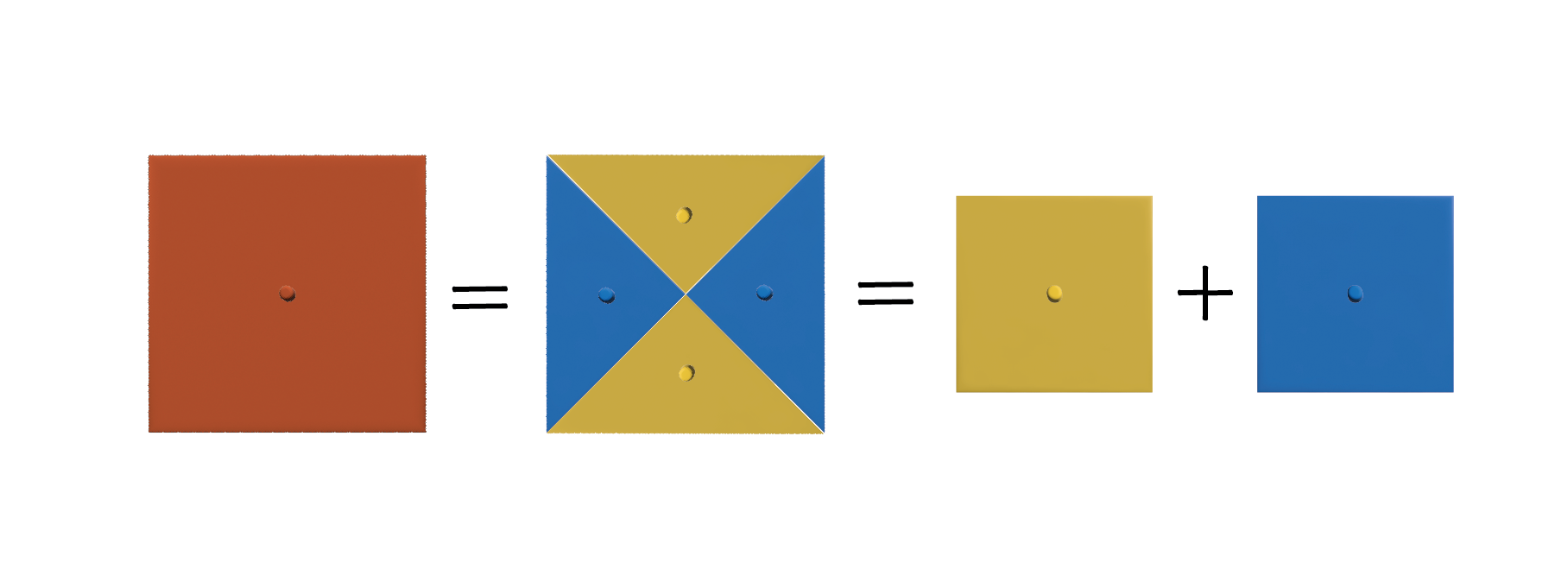
これはまさに三平方の定理が示している内容です。

上図のように辺の長さを$a,b,c$としてパズルの白い三角形と見比べます。

• 青の正方形の面積 $= a^2$
• 黄色の正方形の面積 $= b^2$
• 赤の正方形の面積 $= c^2$

よってパズルの操作から得られた結果
「大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積」は、
三平方の定理$a^2+b^2=c^2$を示しています。

② 辺の長さが3対4対5の直角三角形の場合

工作キット②で作成した教具を使います。
次の図で全てのピースが揃っているか確認できます。

1つ目のパズルと同様に赤い大きな正方形のピースを黄色と青のピースで置き換えるという方針で操作を行っていきます。

最初に次の図のようにピースを並べます。

１つ赤のピースを外し下に置きます。空いたスペースに黄色のピースを置きます。

黄色のピースがなくなってできたスペースに新たな赤いピースを置きます。赤いピースがなくなってできたスペースに新たな黄色のピースを置きます。

この操作を繰り返し、黄色のピースが全て赤のピースと交換された状態になります。

青についても同様に交換を行います。

最後にできたスペースには最初に外した赤のピースを置きます。

全てのピースが過不足なく納まりました。

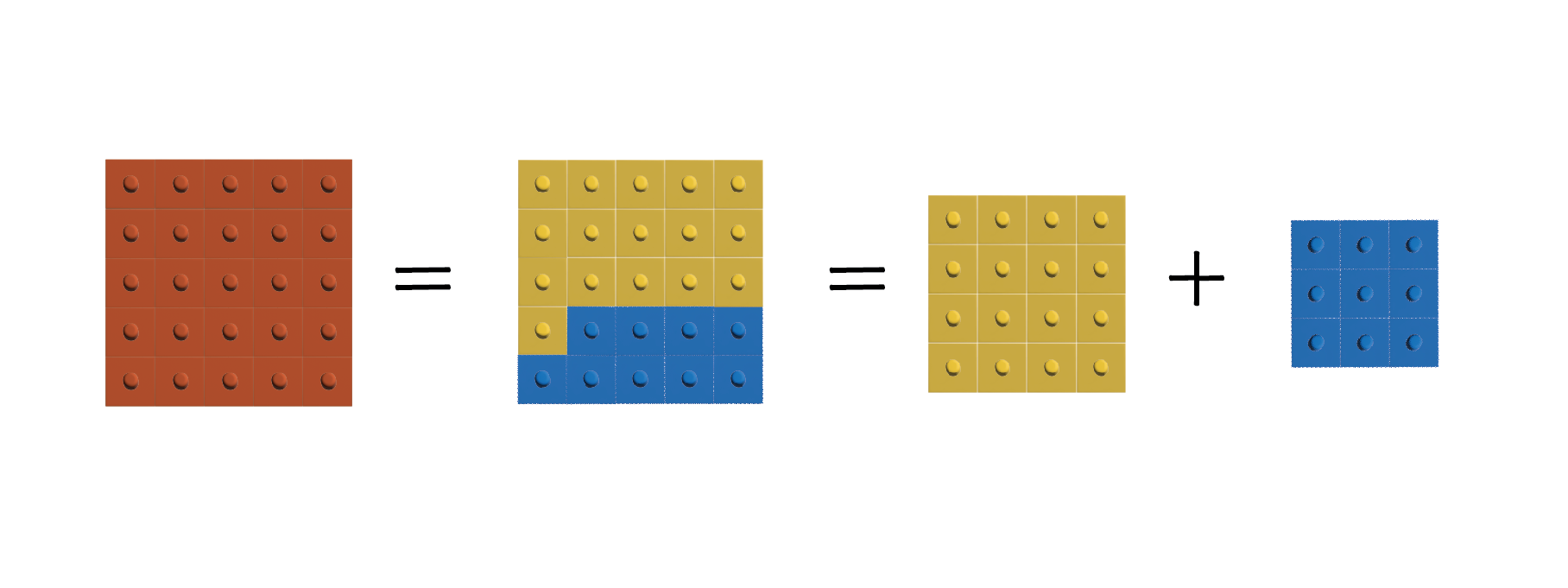
以上で次のことがわかります。

• 大きな赤の正方形の面積 $=$ 赤のピース25個の面積
• 赤のピース25個の面積 $=$ 青のピース9個の面積 $+$ 黄色のピース16個の面積
• 青のピース9個の面積 $+$ 黄色のピース16個の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積

よって次のことがわかります。

• 大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積

直角二等辺三角形の場合と同様に、上図のように辺の長さを$a,b,c$としてパズルの白い三角形と見比べます。

• 青の正方形の面積 $= a^2$
• 黄色の正方形の面積 $= b^2$
• 赤の正方形の面積 $= c^2$

よってパズルの操作から得られた結果
「大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積」は、
三平方の定理$a^2+b^2=c^2$を示しています。

③ 全ての直角三角形の場合

工作キット③で作成した教具を使います。
次の図で全てのピースが揃っているか確認できます。

このパズルを使った証明方法は複数ありますが、ここでは真ん中の枠だけを使う方法を見ていきます。両側に２つある縦長の長方形の枠はここでは無視してください。

最初に図のようにピースを並べます。

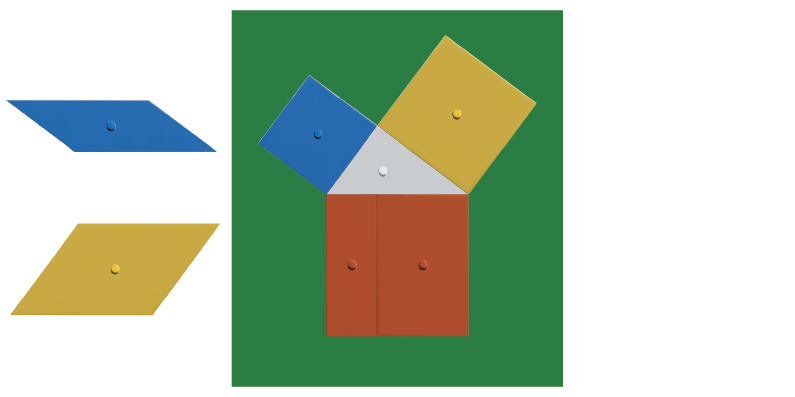
赤の２つの長方形を枠外に置きます。中心にある白い直角三角形を枠の下までズラします。

できたスペースに青の平行四辺形と黄色の平行四辺形を置きます。

ピッタリとはまって、赤の２つのピースの面積が青の平行四辺形の面積と黄色の平行四辺形の面積の和に等しいことがわかりました。

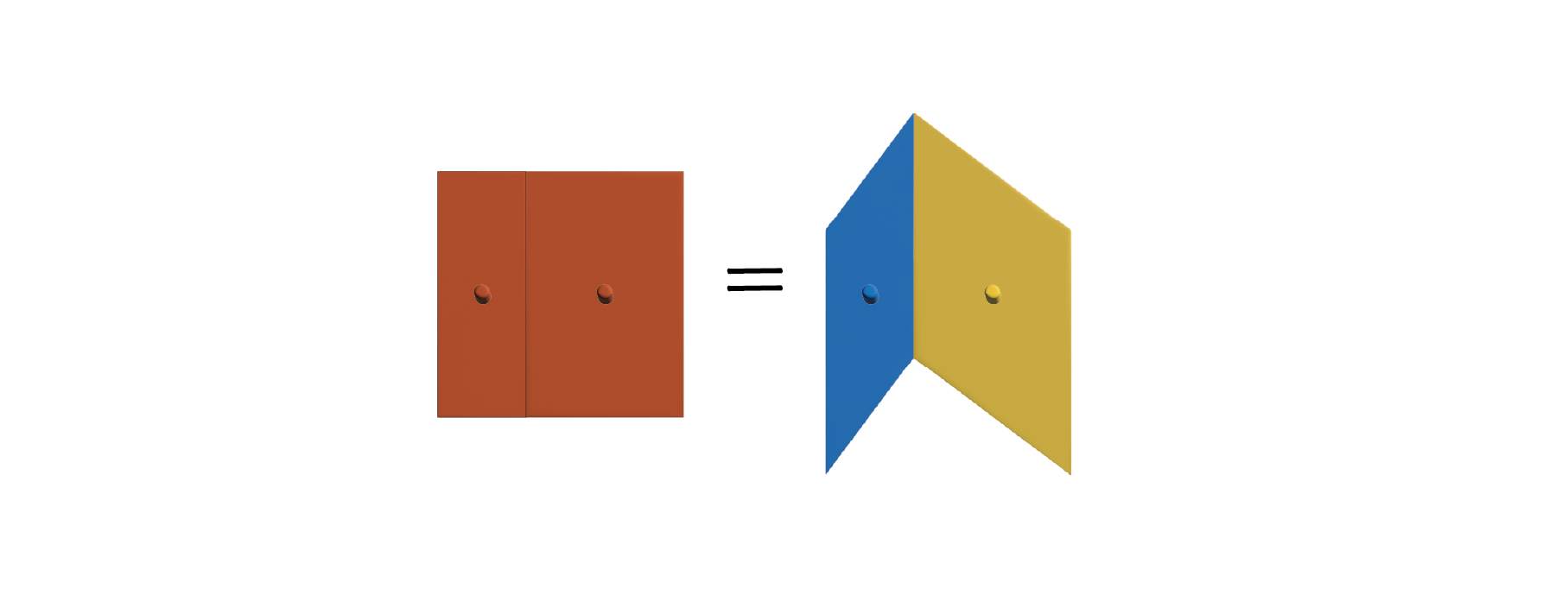
最初の状態に戻します。

黄色の正方形を枠外に置きます。中心にある白い直角三角形を枠の右上までズラします。

できたスペースに黄色の平行四辺形を置きます。

ピッタリとはまって、黄色の正方形の面積が黄色の平行四辺形の面積に等しいことがわかりました。

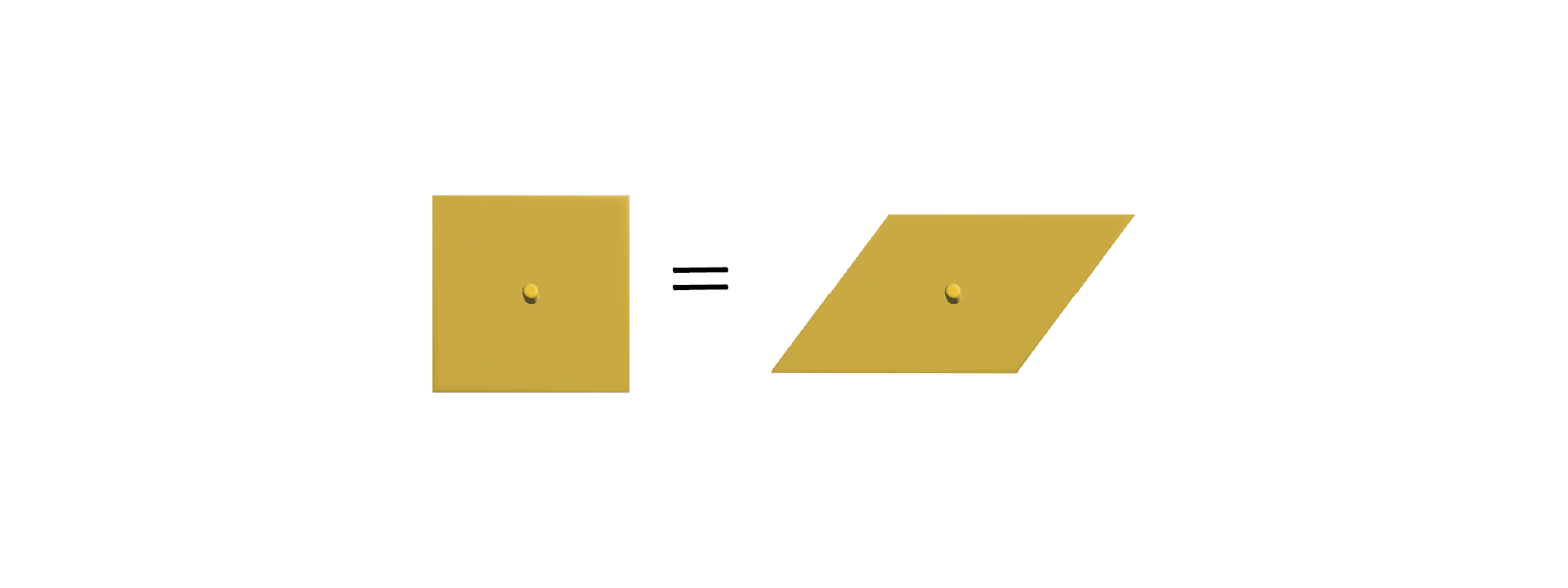
最初の状態に戻します。

青の正方形を枠外に置きます。中心にある白い直角三角形を枠の左上までズラします。

できたスペースに青の平行四辺形を置きます。

ピッタリとはまって、青の正方形の面積が青の平行四辺形の面積に等しいことがわかりました。

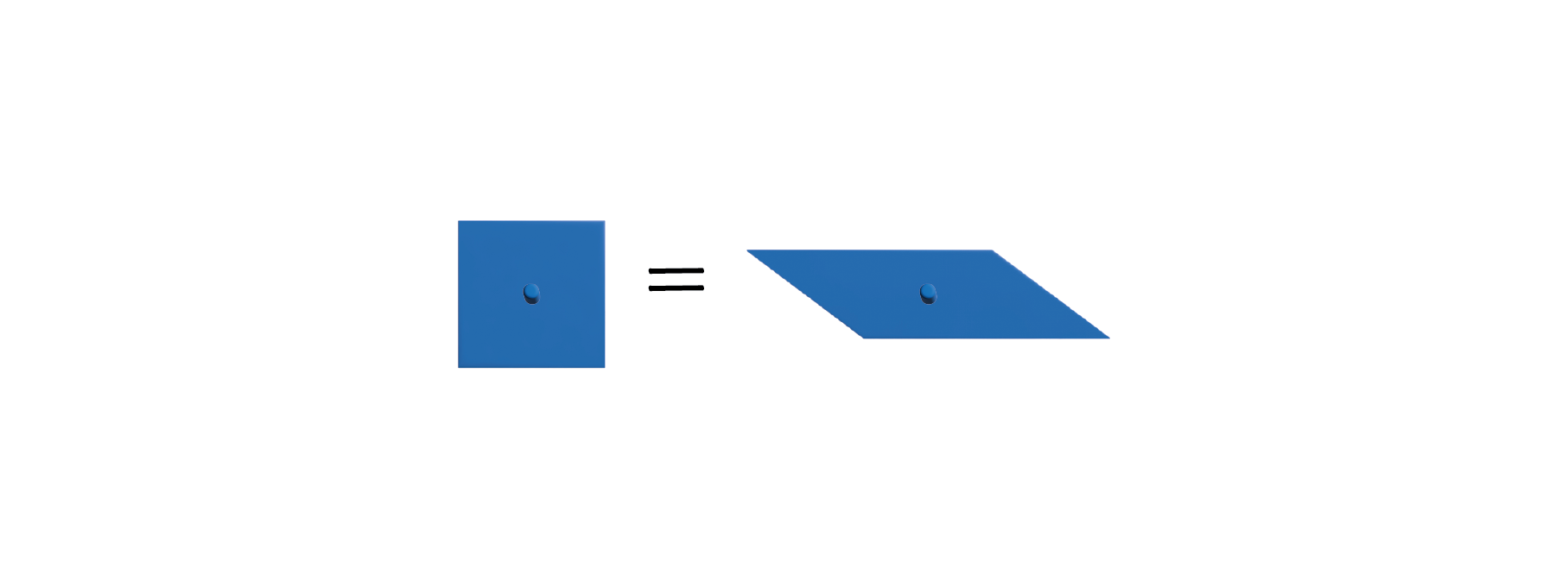
以上により、青と黄色の平行四辺形を仲介として、以下のことが示されました。

• 大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積

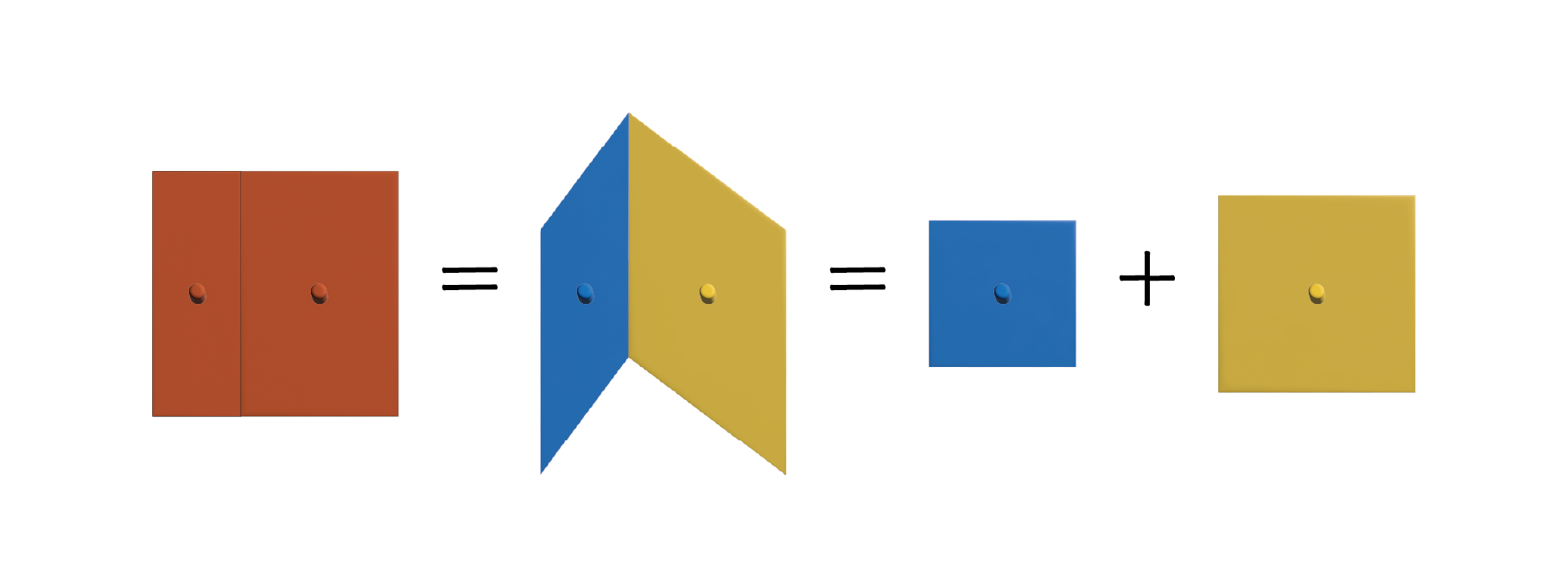
これまでの場合と同様に、辺の長さを$a,b,c$としてパズルの白い三角形と見比べます。

• 青の正方形の面積 $= a^2$
• 黄色の正方形の面積 $= b^2$
• 赤の正方形の面積 $= c^2$

よってパズルの操作から得られた結果
「大きな赤の正方形の面積 $=$ 青の正方形の面積 $+$ 黄色の正方形の面積」は、
三平方の定理$a^2+b^2=c^2$を示しています。

エウクレイデスの三平方の定理の証明

次の動画はエウクレイデスの三平方の定理の証明を表しています。
教具を扱った後で見ると、発見があるかもしれません。

まとめ

ここまで読んでくださった方、ありがとうございました。操作の説明が長くてフォローするのが大変だったと思いますが、大事なことは、こどもたちが自分の手で試行錯誤をして、自分で何かを発見するということに尽きます。

優れた数学的頭脳の持ち主の中には、数学的な厳密性など気になる点が多々あると思います。しかし、こどもたちにとって数学を学ぶということは、「フランスに住んでフランス語を自然と身につけるように、数学の国に住んで数学に親しむということである」とシーモア・パパートは言っていますし³、「偉大な創造物は数学的な心から生まれるので、私たちは常に数学を精神の発展手段と考えなければならない」とマリア・モンテッソーリは言っています⁴。

こどもたちの好奇心や探究心は無限大です。それらが適切に扱われ、善なる方向に凝縮されるとき、社会ひいては文明レベルで大きな平和的進歩が得られることは自明の理だと思います。ポリマスリサーチでは、ヒトの万能性に着目した発達理論研究と、その理論研究に基づいた環境整備を非営利活動として進めていきます。応援のほど、よろしくお願いします。

遊ぶことで発見の喜びを得る

最後に、小学生の頃にこの教具で学んだウィル・ライト⁵の感想を紹介して筆を擱きます。

「モンテッソーリメソッドは発見の喜びを私に教えてくれた。例えばピタゴラス理論（三平方の定理）のような複雑な理論でも、ブロックで遊ぶことで興味を持つことができる。教師が説明するのではなく、自分で学ぶことが大切なのだ。シムシティはまさにモンテッソーリメソッドから生まれたものだ。」

Seabrook, John (2006年11月6日). “Game Master”. The New Yorkerより引用

---

Footnotes

1. モンテッソーリ教育は一斉教育ではないため、学ぶ時期は子どもによる。今回紹介した三平方の定理の教具は9歳から使用することを想定して作られている。 ↩

2. 『原論』第1巻命題47に三平方の定理の証明が記載されている。 ↩

3. "The idea of “talking mathematics” to a computer can be generalized to a view of learning mathematics in “Mathland”; that is to say, in a context which is to learning mathematics what living in France is to learning French.", Papert, Seymour. Mindstorms: Children, Computers and Powerful Ideas. ↩

4. "Great creations come from the mathematical mind, so we must always consider all that is mathematical as a means of mental development.", Maria Montessori – The Discovery of the Child. ↩

5. アメリカのゲームクリエイター。シミュレーションゲームのシムシティをはじめとするシムシリーズの製作者。 ↩